Secciones
Servicios
Destacamos
Secciones
Servicios
Destacamos

Patricia Cabezuelo
Viernes, 6 de septiembre 2024, 00:05
Ptolomeo escribió su obra 'Geograhia' hacia el siglo II de nuestra era, con una técnica tan avanzada que sirvió de modelo a la cartografía moderna. Desde entonces, la mayoría de los que nos enfrentamos a un mapa pensamos se trata de una ciencia exacta y lo que vemos representados en ellos es tal cual lo que hay. Pero nada más lejos de la realidad.
La simple representación de un cuerpo esférico en una superficie plana ya supone una invención. La Tierra es redonda y plasmarla en un mapa supone el primer embrollo. Siendo estrictamente correctos, tampoco es redonda, no es una esfera perfecta. Los efectos de la gravitación y de la fuerza centrífuga producida al rotar sobre su eje generan el aplanamiento en los polos y un ensanchamiento en el ecuador. Además, su superficie no es plana, no se trata de una bola redonda donde todos los puntos tienen el mismo campo gravitatorio, la misma gravedad, algo que ya predijo Isaac Newton a finales del siglo XVII. Es decir, que ni siquiera es una esfera.
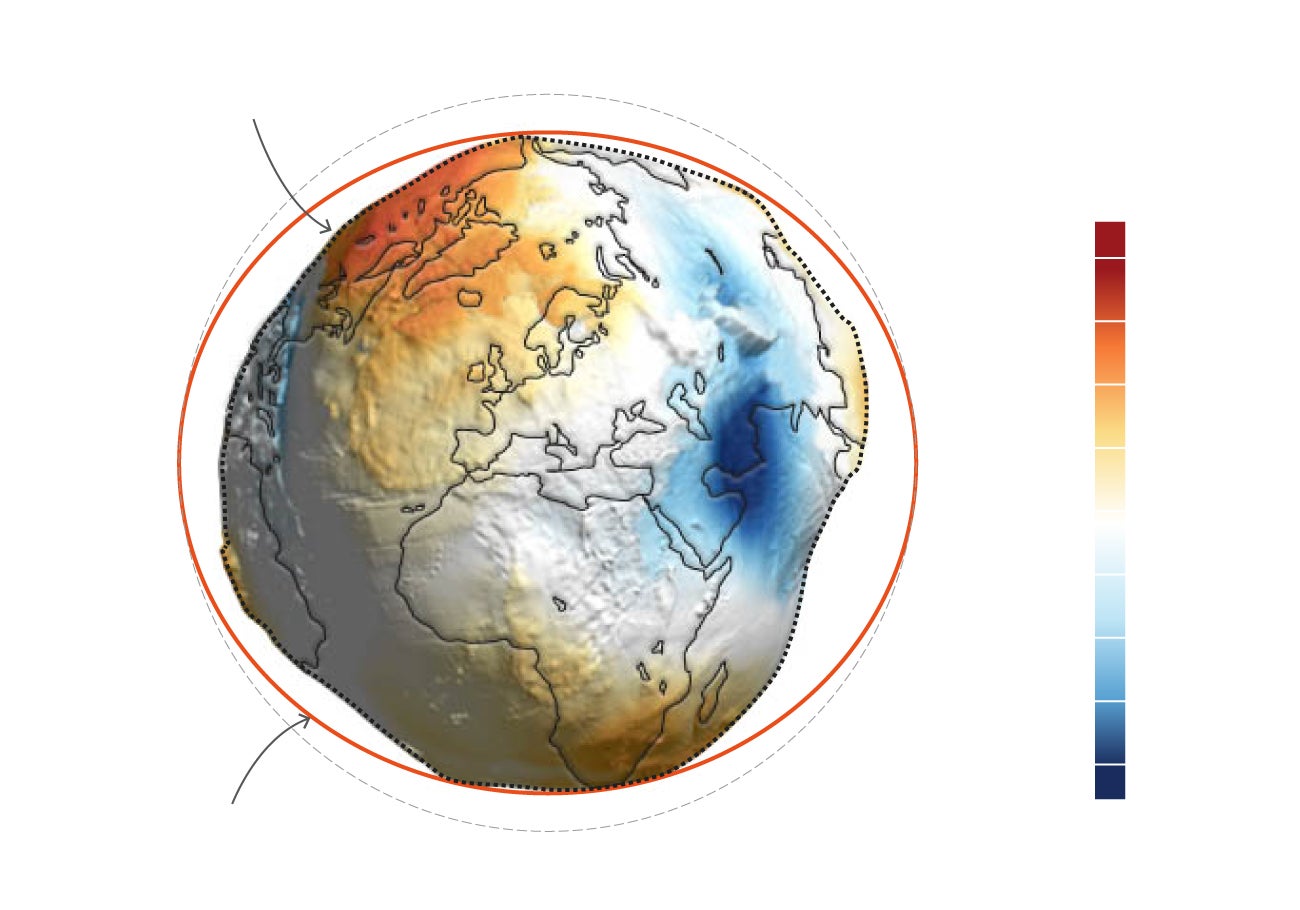
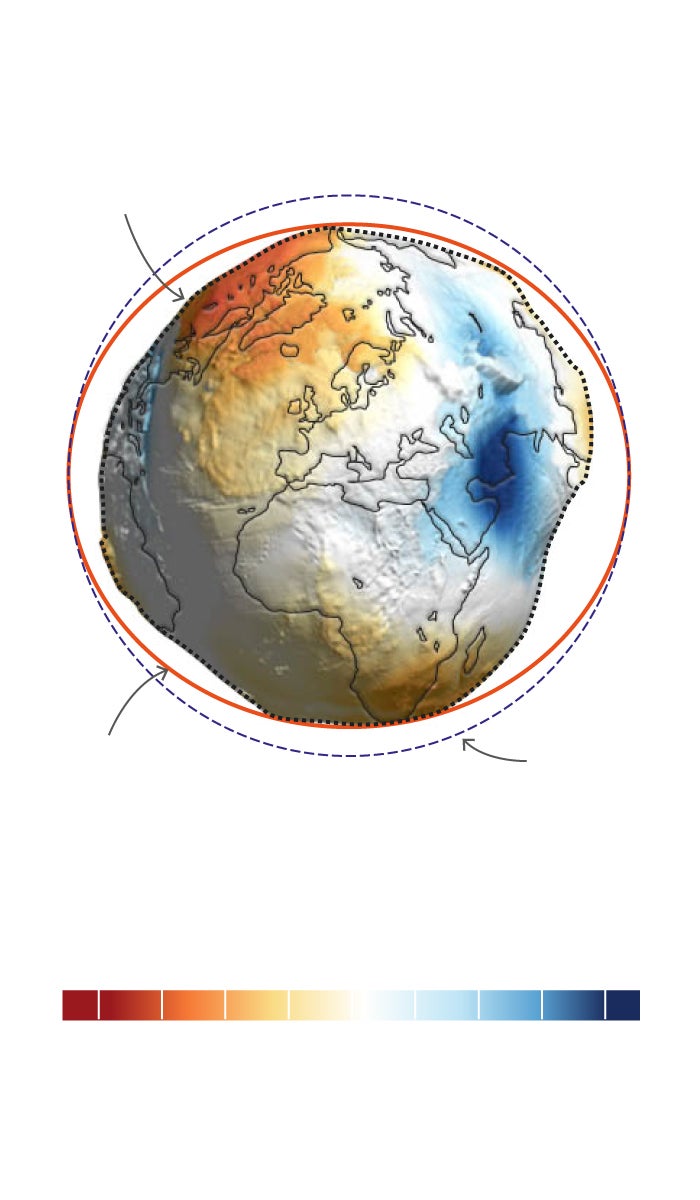
Hay unanimidad en el mundo científico en que la forma más precisa de representarla, más que una esfera o una elipse, es el geoide. El geoide es una superficie física que representa igual campo gravitatorio en toda la superficie y coincide, más o menos, con el nivel medio del mar. Se extiende teóricamente por debajo de los continentes y refleja las irregularidades del campo de gravedad. Así pues el medio más preciso de mostrar cómo es la Tierra es esta forma teórica muy irregular que sólo se ha podido definir con alta precisión desde los avances en la geodesia satelital a finales del siglo XX.
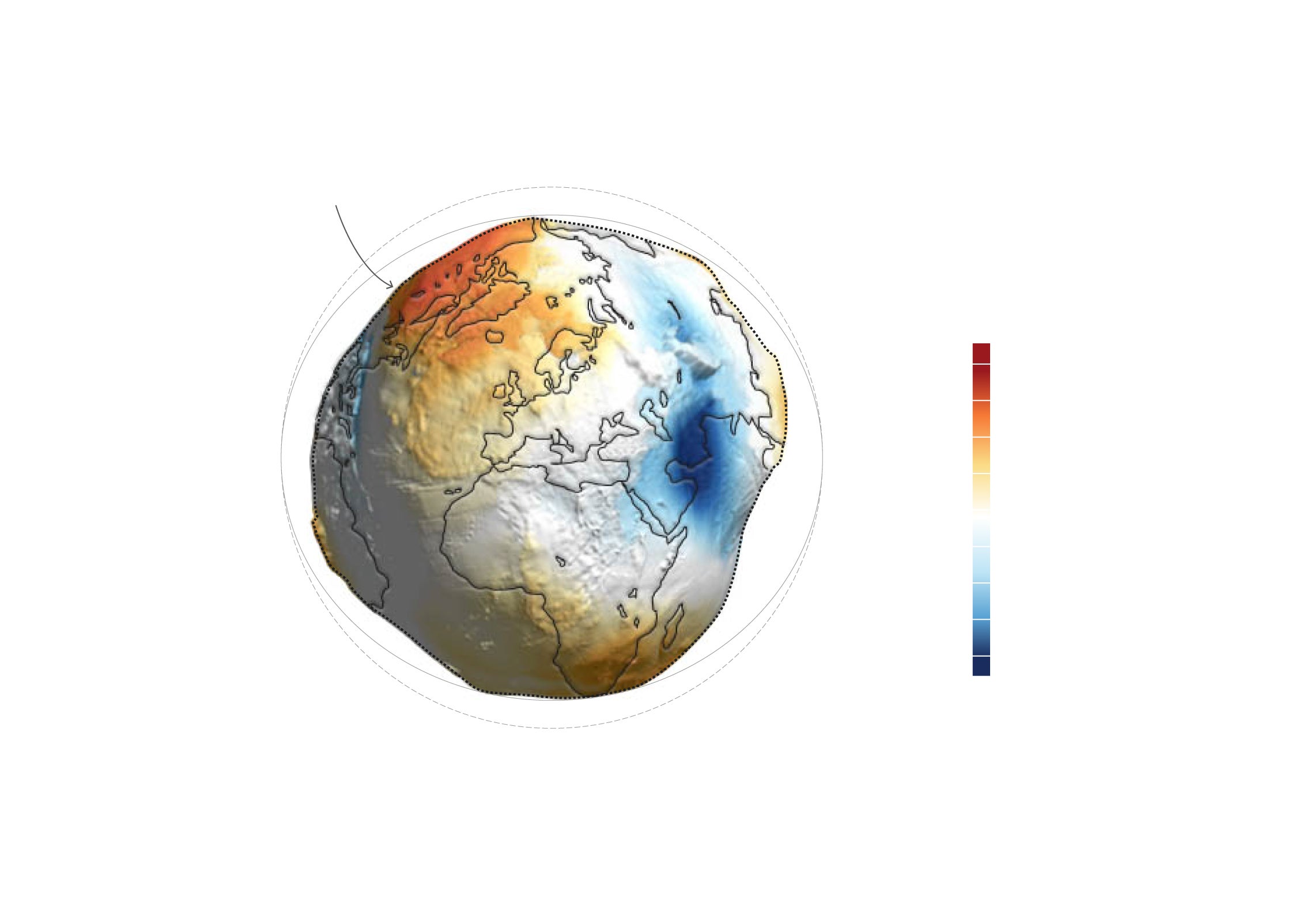
GEOIDE
Altura
del geoide
(m)
80
60
40
20
0
-20
-40
-60
-80
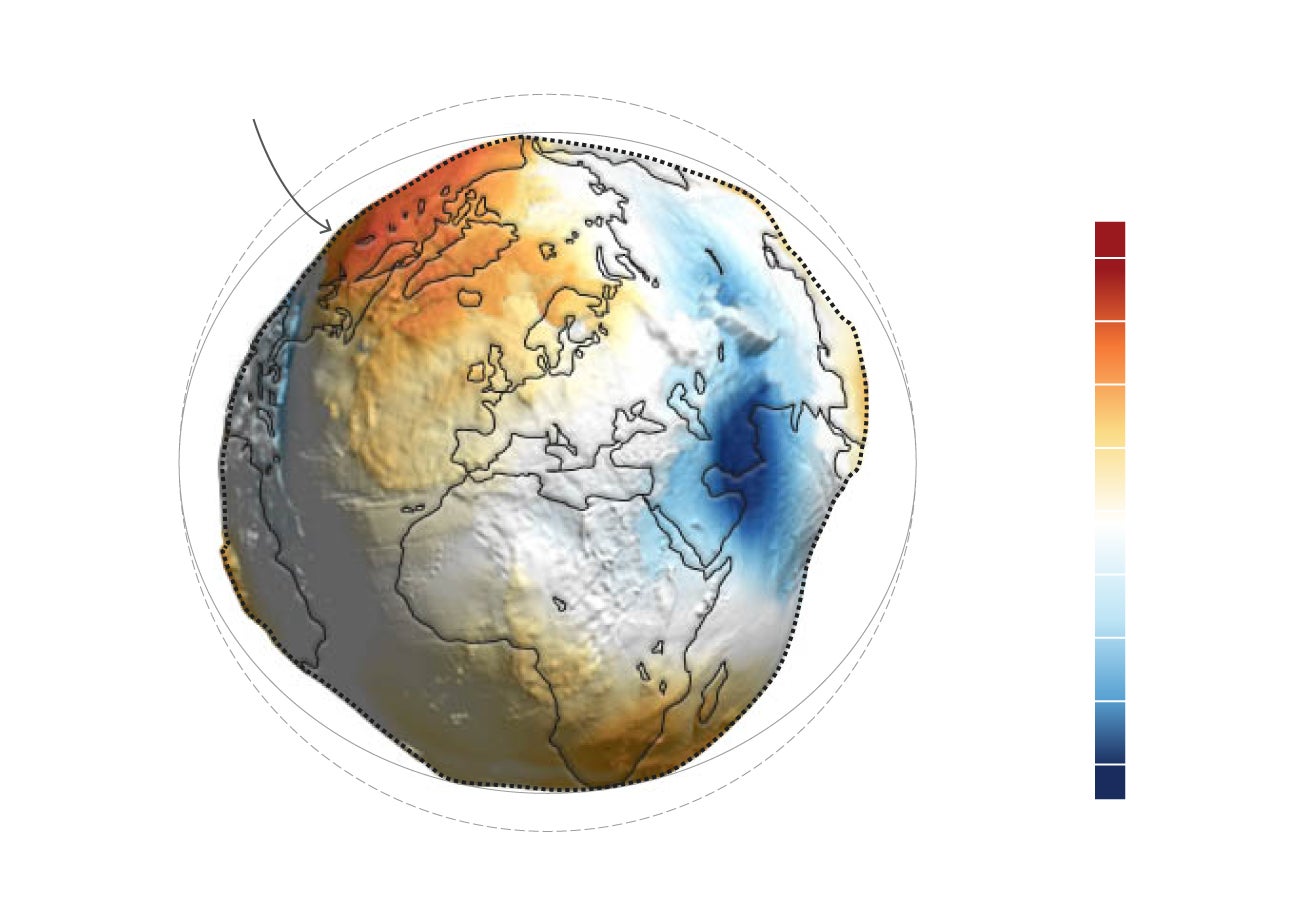
GEOIDE
Altura
del geoide
(m)
80
60
40
20
0
-20
-40
-60
-80
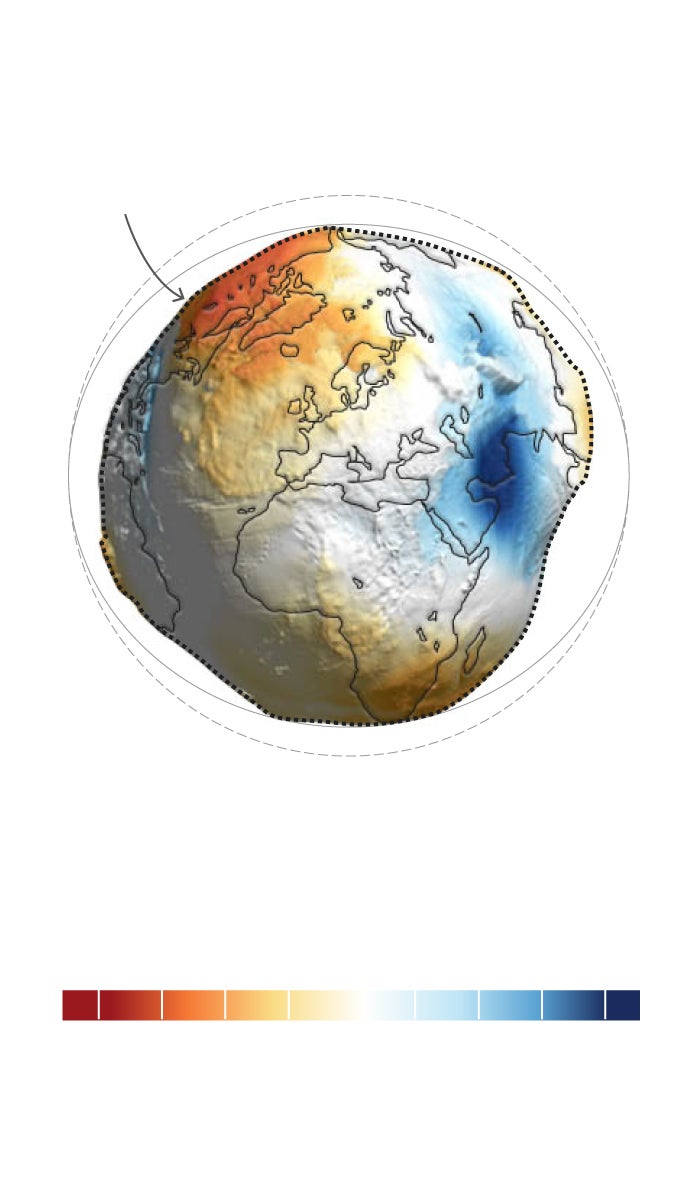
GEOIDE
(m)
ALTURA DEL GEOIDE
80
40
60
20
0
-20
-40
-60
-80
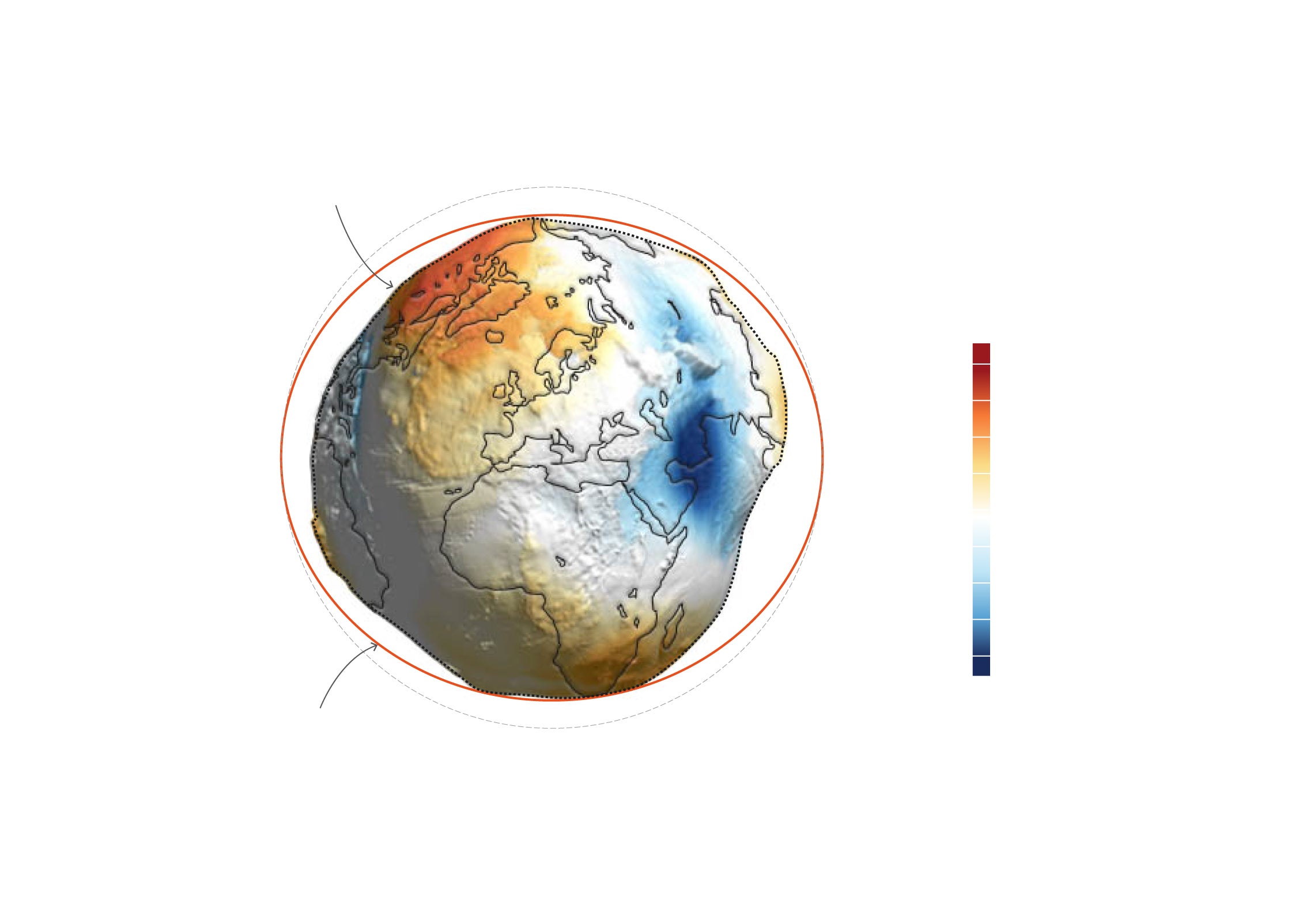
GEOIDE
Altura
del geoide
(m)
80
60
40
20
0
-20
-40
-60
-80
Elipsoide
GEOIDE
Altura
del geoide
(m)
80
60
40
20
0
-20
-40
-60
-80
Elipsoide
GEOIDE
Elipsoide
(m)
ALTURA DEL GEOIDE
80
40
60
20
0
-20
-40
-60
-80
GEOIDE
Altura
del geoide
(m)
80
60
40
20
0
-20
-40
-60
-80
Elipsoide
Esfera
GEOIDE
Altura
del geoide
(m)
80
60
40
20
0
-20
-40
-60
-80
Elipsoide
Esfera
GEOIDE
Elipsoide
Esfera
(m)
ALTURA DEL GEOIDE
80
40
60
20
0
-20
-40
-60
-80
Es la representación de la forma esferoidal e irregular de la Tierra. Las deformidades plasman distintas presiones gravitoatorias similares a altitudes. El punto más alto sería +85 en Islandia y -106m al sur de la India y no se deben confundir con las altitudes reales (+8.800 del Everest a los -11.000m de la Fosa de las Marianas). Esta superficie irregular no permite hacer cálculos geométricos precisos
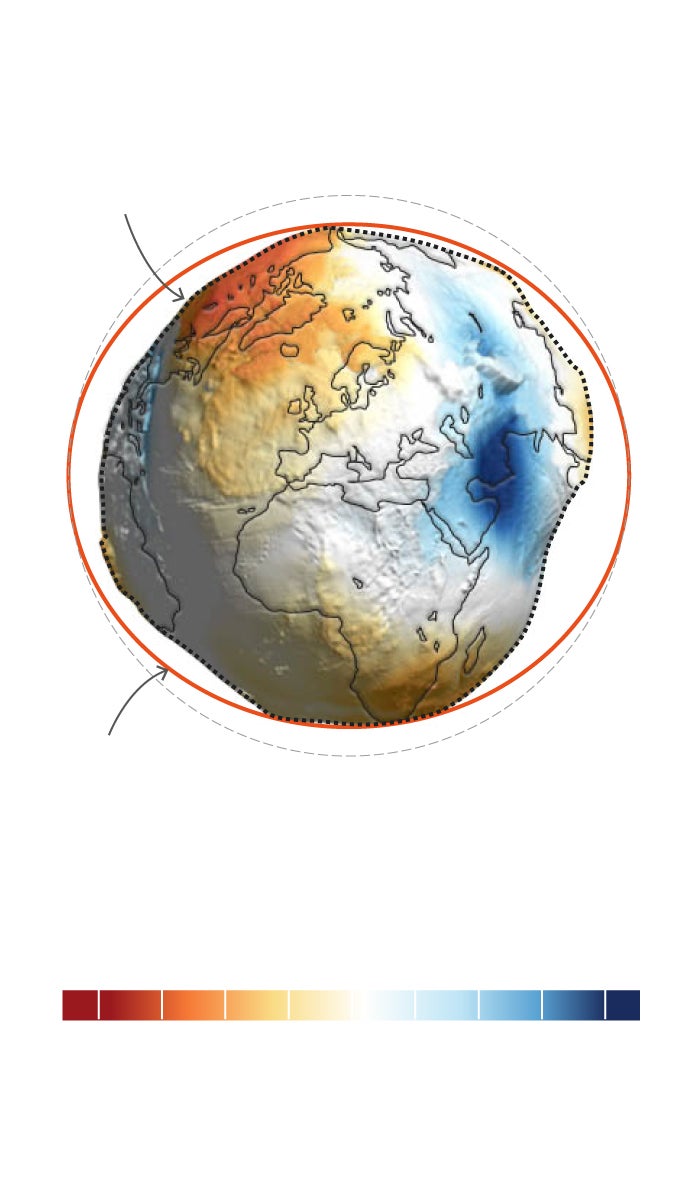
Como el geoide no permite hacer cálculos matemáticos exactos, para representar la Tierra se utiliza la figura matemática más próxima: el elipsoide. Una esfera achatada por los polos que permite asignar coordenadas a un punto sobre la superficie terrestre y realizar operaciones
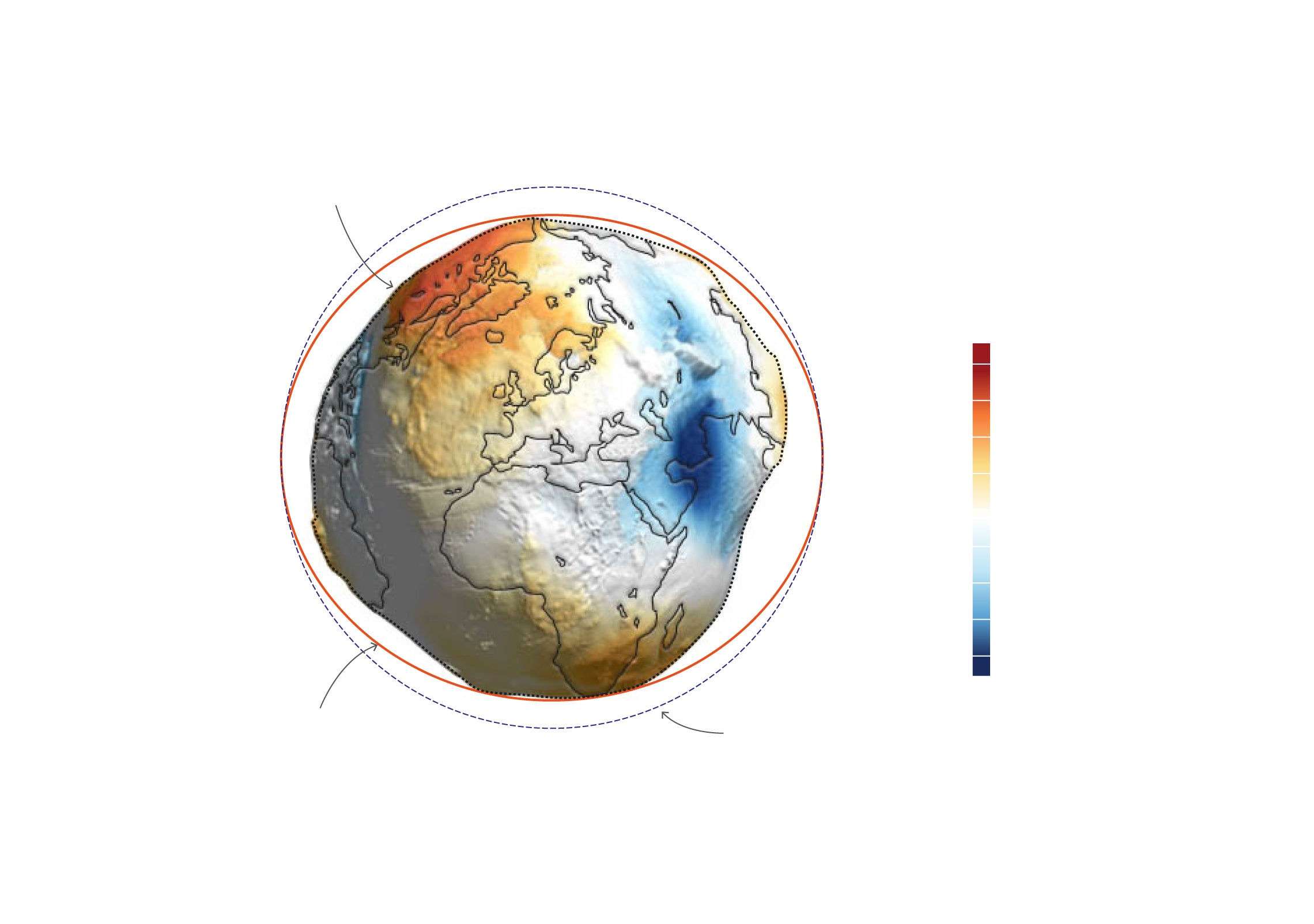
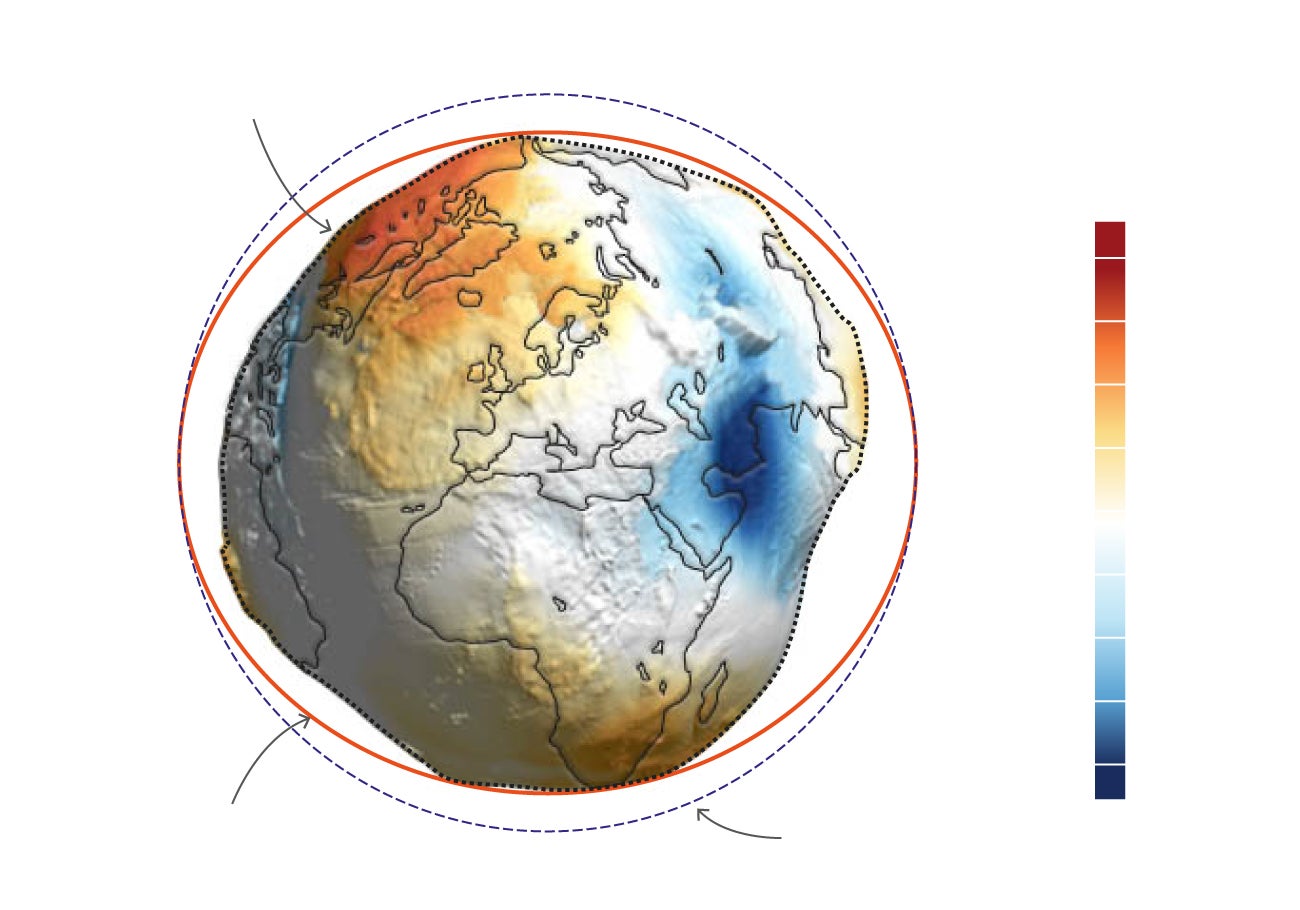
Si tomamos como referencia una esfera perfecta y el geoide, vemos que la típica canica azul no encaja ni mucho menos con la forma real de la Tierra
AUX STEP FOR JS
Volvamos a la cartografía. Al transferir la imagen tridimensional de la Tierra y sus irregularidades a una superficie plana, bidimensional, es necesario considerar las distorsiones que van a surgir. Por eso es imprescindible comprender el geoide. Pero también necesitamos conocer el sistema de referencia de coordenadas que se va a utilizar. Este sistema de referencia de coordenadas es un marco que define cómo se expresan los puntos en el espacio y depende del sistema de coordenadas y del sistema de referencia geodésico. Palabras aparentemente complejas pero que esconden una realidad sencilla.

SISTEMA DE COORDENADAS
Método para determinar la posición
de un punto en el espacio
+
SISTEMA DE REFERENCIA
GEODÉSICO
Es cómo se proyecta la Tierra
en dos dimensiones
=
SISTEMA DE REFERENCIA
DE COORDENADAS (CRS)
Debe constar en todas las cartografías
para poder interpretar correctamente
la información que contienen

SISTEMA DE COORDENADAS
Método para determinar la posición
de un punto en el espacio
+
SISTEMA DE REFERENCIA GEODÉSICO
Es cómo se proyecta la Tierra
en dos dimensiones
=
SISTEMA DE REFERENCIA
DE COORDENADAS (CRS)
Debe constar en todas las cartografías
para poder interpretar correctamente
la información que contienen
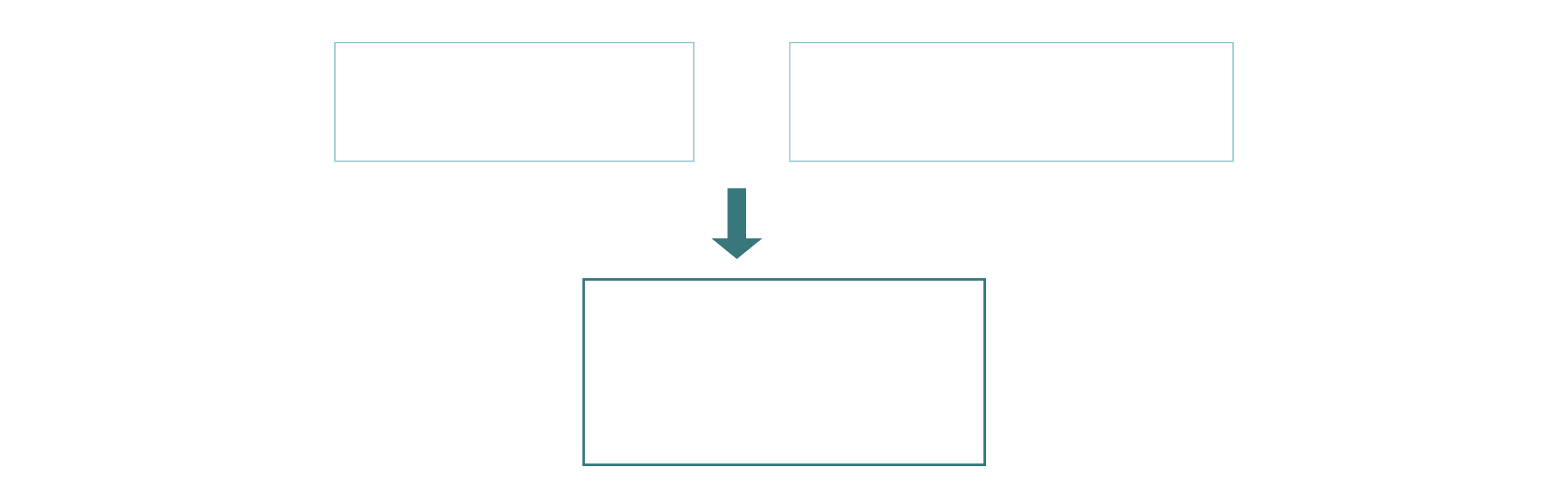
SISTEMA DE REFERENCIA GEODÉSICO
SISTEMA DE COORDENADAS
+
Método para determinar la posición
de un punto en el espacio
Es cómo se proyecta la Tierra
en dos dimensiones
SISTEMA DE REFERENCIA
DE COORDENADAS (CRS)
Debe constar en todas las cartografías
para poder interpretar correctamente
la información que contienen

SISTEMA DE REFERENCIA
DE COORDENADAS (CRS)
SISTEMA DE REFERENCIA GEODÉSICO
=
SISTEMA DE COORDENADAS
+
Debe constar en todas las cartografías
para poder interpretar correctamente
la información que contienen
Método para determinar la posición
de un punto en el espacio
Es cómo se proyecta la Tierra
en dos dimensiones
Los sistemas de coordenadas permiten conocer la posición de puntos en el espacio y realizar cálculos imprescindibles para el transporte, las infraestructuras, la física... Hay dos grupos de sistemas de coordenadas, las que sirven para objetos tridimensionales y las planas o cartesianas que sirven para objetos bidimensionales; es decir, mapas o planos.Las primeras utilizan longitud y latitud que son ángulos que se miden desde el centro de la Tierra a un punto de la superficie. Por eso la unidad de medida son grados decimales; mientras que las segundas utilizan los metros y se basan en los ejes x e y.

Geográficas
EJEMPLO
Este punto estaría a 40 grados
latitud norte y 50 grados
longitud este
50
40
30
Ecuador
20
latitud
10
0
10
40
20
30
longitud
Meridiano de
Greenwich
UNIDADES DE MEDIDA
Longitud
Mide el ángulo desde el meridiano
de Greenwich que es 0º hasta +/- 180°
Latitud
Mide el ángulo norte o sur del Ecuador,
que es 0° y +/- 90° en los polos
Altitud
Altura sobre el nivel del mar o sobre
el geoide
Proyectadas
Transforman coordenadas geográficas
en coordenadas planas (x, y) para
representar áreas en mapas planos
UNIDAD
DE MEDIDA
Metros
Se pasa de una
superficie curva a una plana
ELEMENTOS
Coordenadas
Sistema de líneas horizontales (paralelos)
y verticales (meridianos)
Escala y rosa de los vientos
Es esencial para medir distancias y
calcular áreas en el mapa y saber
dónde está el norte

Geográficas
EJEMPLO
Este punto estaría a
40 grados latitud norte
y 50 grados longitud este
50
40
30
Ecuador
20
latitud
10
0
10
40
20
30
longitud
Meridiano de
Greenwich
UNIDADES DE MEDIDA
Longitud
Mide el ángulo desde el meridiano
de Greenwich que es 0º hasta +/- 180°
Latitud
Mide el ángulo norte o sur del Ecuador,
que es 0° y +/- 90° en los polos
Altitud
Altura sobre el nivel del mar o sobre
el geoide
Proyectadas
Transforman coordenadas geográficas
en coordenadas planas (x, y) para
representar áreas en mapas planos
UNIDAD
DE MEDIDA
Metros
Se pasa de una
superficie curva a una plana
ELEMENTOS
Coordenadas
Sistema de líneas horizontales (paralelos)
y verticales (meridianos)
Escala y rosa de los vientos
Es esencial para medir distancias y
calcular áreas en el mapa y saber
dónde está el norte
Proyectadas
Geográficas
EJEMPLO
Transforman coordenadas geográficas
en coordenadas planas (x, y) para
representar áreas en mapas planos
Este punto estaría a
40 grados latitud norte
y 50 grados longitud este
50
40
30
Ecuador
20
latitud
10
0
10
40
20
30
longitud
Meridiano de
Greenwich
UNIDAD
DE MEDIDA
Metros
UNIDADES DE MEDIDA
Se pasa de una
superficie curva a una plana
Longitud
Mide el ángulo desde el meridiano de
Greenwich que es 0º hasta +/- 180°
ELEMENTOS
Coordenadas
Latitud
Sistema de líneas horizontales (paralelos)
y verticales (meridianos)
Mide el ángulo norte o sur del Ecuador,
que es 0° y +/- 90° en los polos
Escala y rosa de los vientos
Altitud
Es esencial para medir distancias y
calcular áreas en el mapa y saber
dónde está el norte
Altura sobre el nivel del mar o sobre
el geoide
Proyectadas
Geográficas
EJEMPLO
Transforman coordenadas geográficas en coordenadas planas (x, y)
para representar áreas en mapas planos
Este punto estaría a
40 grados latitud norte
y 50 grados longitud este
UNIDAD
DE MEDIDA
50
40
Metros
30
UNIDADES DE MEDIDA
Se pasa de una
superficie curva a una plana
Ecuador
20
Longitud
latitud
10
Mide el ángulo desde el meridiano
de Greenwich que es 0º hasta +/- 180°
ELEMENTOS
0
10
40
20
30
Coordenadas
longitud
Latitud
Sistema de líneas horizontales (paralelos)
y verticales (meridianos)
Mide el ángulo norte o sur del Ecuador,
que es 0° y +/- 90° en los polos
Escala y rosa de los vientos
Altitud
Es esencial para medir distancias y
calcular áreas en el mapa y saber
dónde está el norte
Meridiano de
Greenwich
Altura sobre el nivel del mar o sobre
el geoide
Para representar la Tierra en dos dimensiones, que es el tema que nos ocupa, hay que proyectarla con un sistema de referencia geodésico. Esto significa utilizar un conjunto de reglas y herramientas que dependiendo de la proyección elegida presentan mejor unas zonas u otras. Aquí es donde empiezan 'las mentiras'.
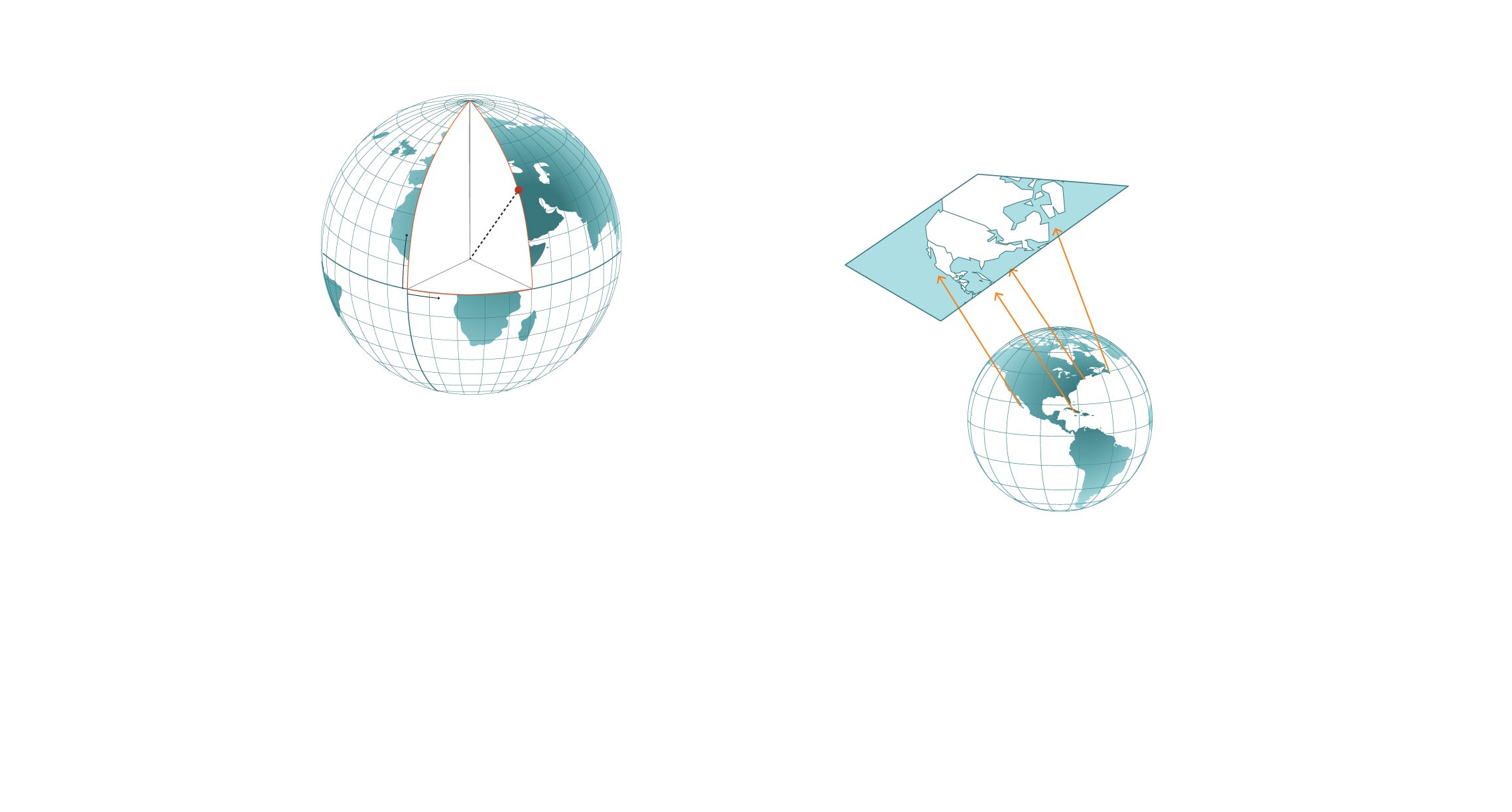
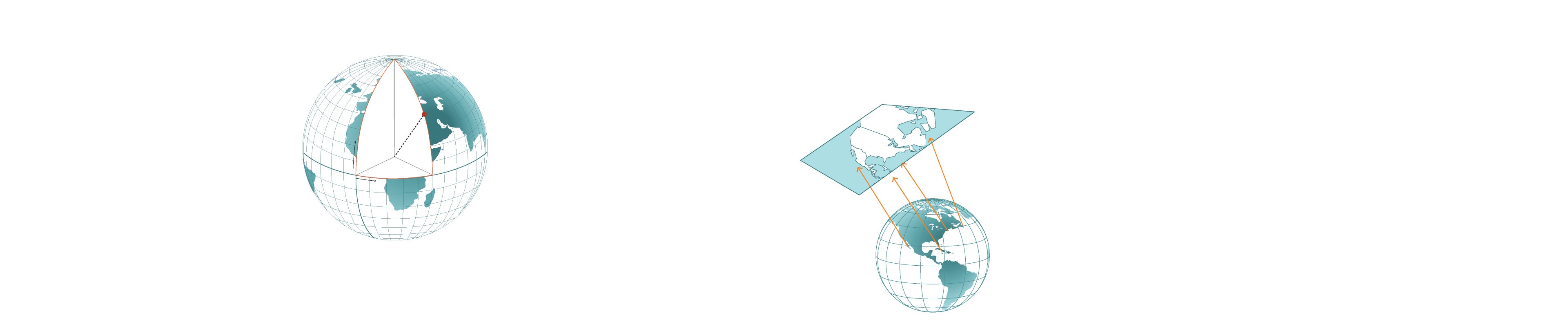
Básicamente hay tres tipos de proyecciones: cilíndricas, cónicas y planares o azimutales.
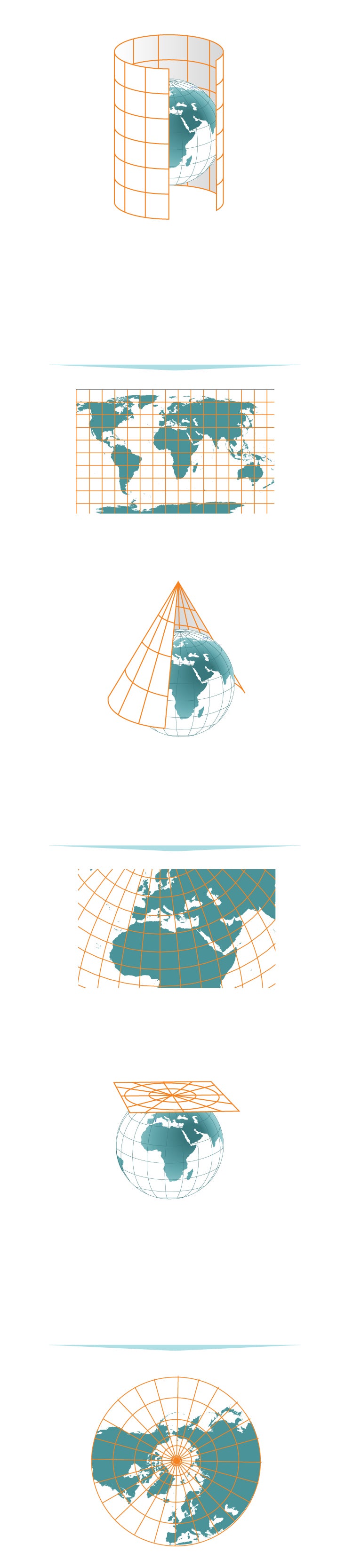
Cilíndricas
Es como si envolviéramos el globo en una hoja de papel con forma de cilindro y se tranfierieran a ella todas las características geográficas. Al aplanar la hoja obtendríamos el mapa con una retícula rectangular de paralelos y meridianos
Cónicas
Método para proyectar mapas en un cono circundante, que luego se aplana hasta formar una superficie con círculos concéntricos como paralelos y líneas irradiadas desde los meridianos
Azimutales/planares
En esta proyección cartográfica se supone que la Tierra descansa sobre una superficie plana sobre la que se proyectan sus características. Un papel plano debe tocar el globo en un punto y proyectar las líneas de latitud y longitud en un plano
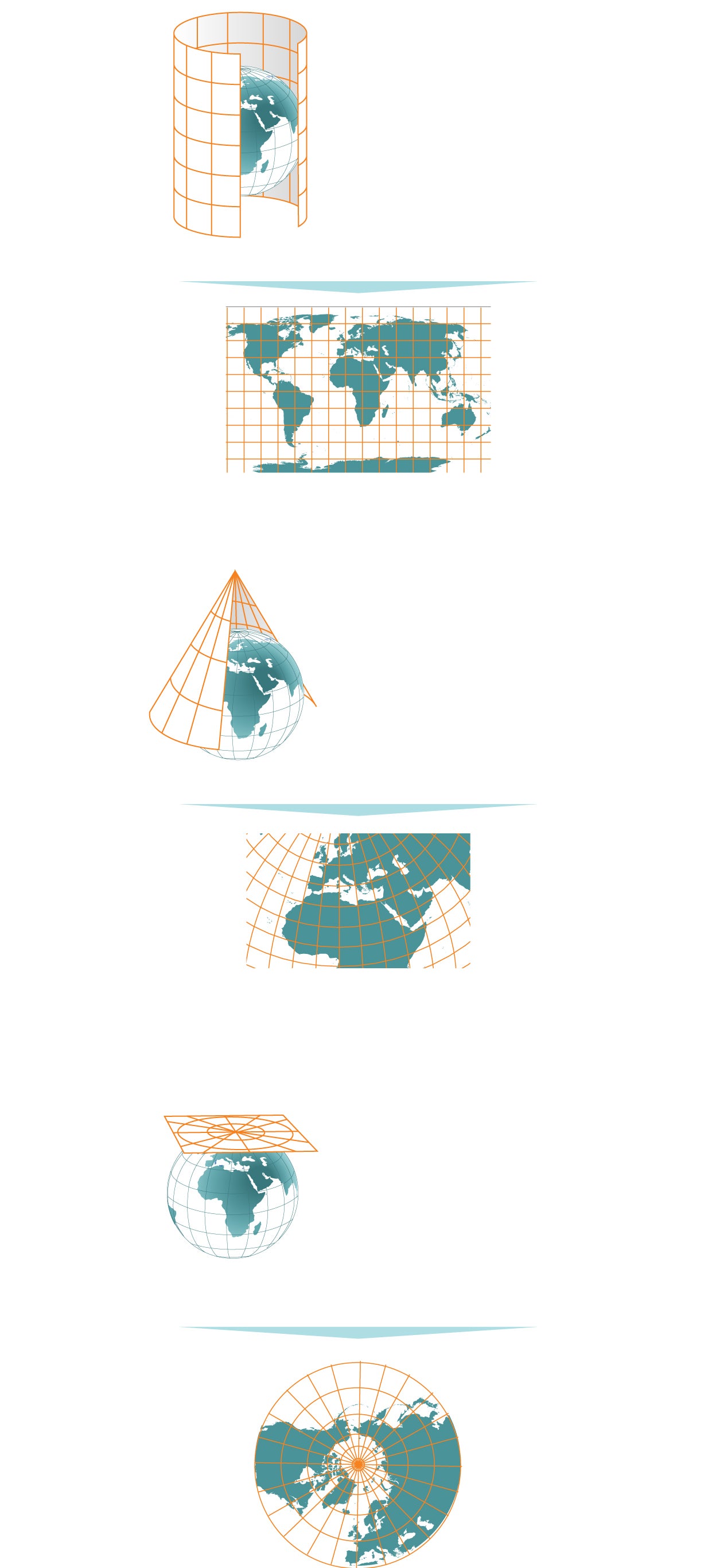
Cilíndricas
Es como si envolviéramos el globo en una hoja de papel con forma de cilindro y se tranfierieran a ella todas las características geográficas. Al aplanar la hoja obtendríamos el mapa con una retícula rectangular de paralelos y meridianos
Cónicas
Método para proyectar mapas en un cono circundante, que luego se aplana hasta formar una superficie con círculos concéntricos como paralelos y líneas irradiadas desde los meridianos
Azimutales/planares
En esta proyección cartográfica se supone que la Tierra descansa sobre una superficie plana sobre la que se proyectan sus características. Un papel plano debe tocar el globo en un punto y proyectar las líneas de latitud y longitud en un plano
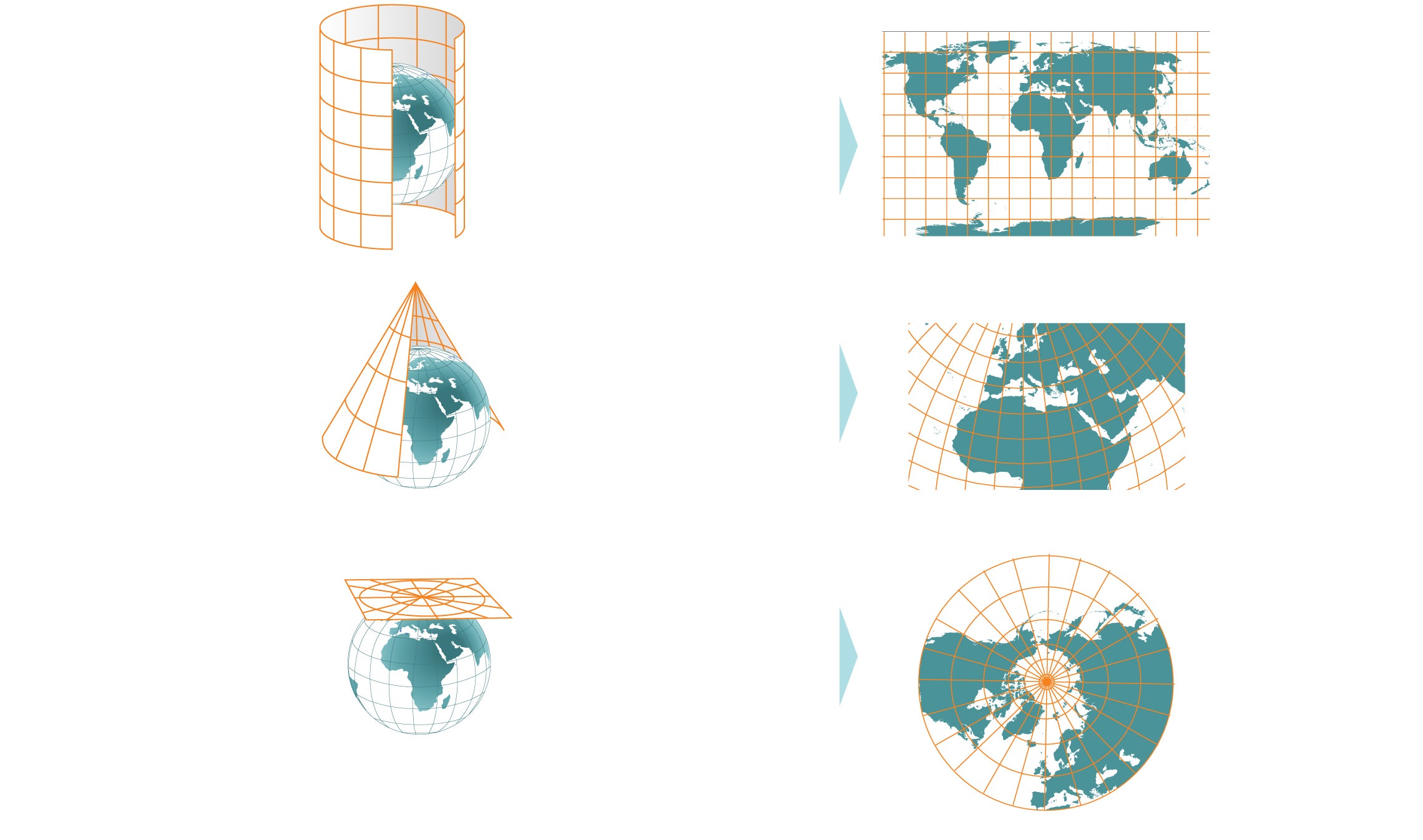
Cilíndricas
Es como si envolviéramos el globo en una hoja de papel con forma de cilindro y se tranfierieran a ella todas las características geográficas. Al aplanar la hoja obtendríamos el mapa con una retícula rectangular de paralelos y meridianos
Cónicas
Método para proyectar mapas en un cono circundante, que luego se aplana hasta formar una superficie con círculos concéntricos como paralelos y líneas irradiadas desde los meridianos
Azimutales/planares
En esta proyección cartográfica se supone que la Tierra descansa sobre una superficie plana sobre la que se proyectan sus características. Un papel plano debe tocar el globo en un punto y proyectar las líneas de latitud y longitud en un plano
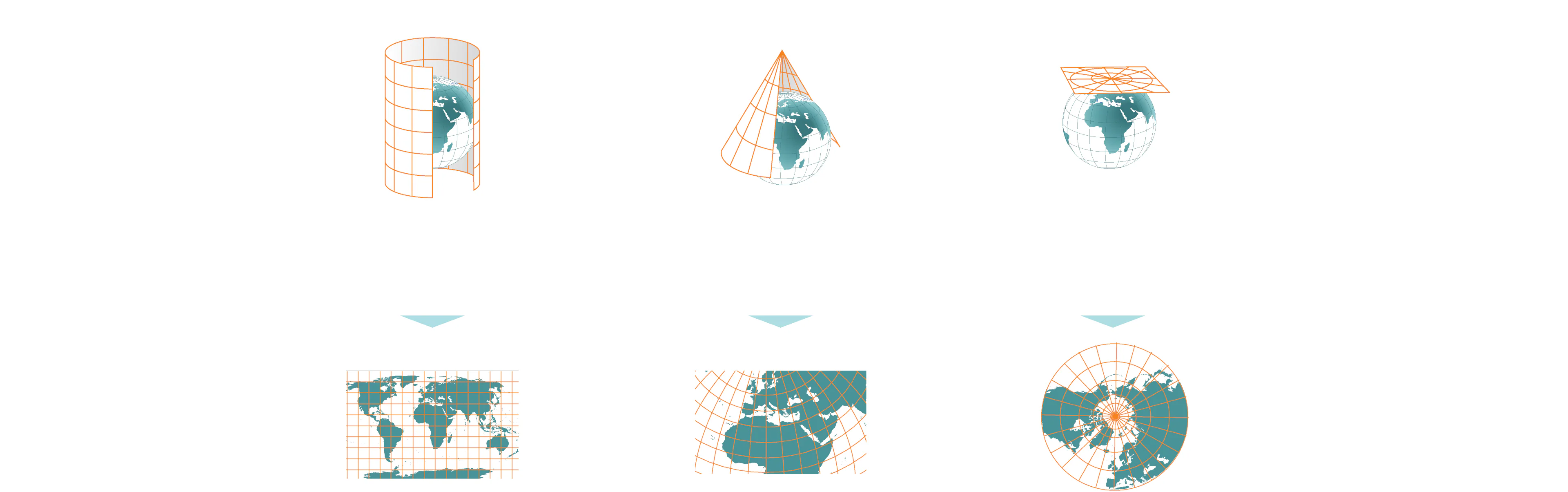
Azimutales/planares
Cilíndricas
Cónicas
Es como si envolviéramos el globo en una hoja de papel con forma de cilindro y se tranfierieran a ella todas las características geográficas. Al aplanar la hoja obtendríamos el mapa con una retícula rectangular de paralelos y meridianos
Método para proyectar mapas en un cono circundante, que luego se aplana hasta formar una superficie con círculos concéntricos como paralelos y líneas irradiadas desde los meridianos
En esta proyección cartográfica se supone que la Tierra descansa sobre una superficie plana sobre la que se proyectan sus características. Un papel plano debe tocar el globo en un punto y proyectar las líneas de latitud y longitud en un plano
La proyección cilíndrica es la mejor para la zona ubicada entre el Ecuador y los trópicos; las cónicas son las idóneas para las zonas templadas, que van de los trópicos a los polos y estos últimos son más exactos si se representan con la proyección azimutal. Según la fórmula escogida algunos países se verán de una forma o de otra, muy distinta.
También hay que tener en cuenta la orientación de la proyección elegida que puede ser normal, transversal u oblicua y que hay sistemas de referencia globales y locales. Estos últimos intentan que un país o zona se muestre con la mayor exactitud posible pero sólo funcionan para pequeñas extensiones.

Cilíndricas
Normal
Transversal
Oblicua
La primera usa las líneas de latitud como líneas de contacto; la segunda, los meridianos y la oblicua otras grandes líneas circulares
Cónicas
Normal
Transversal
Oblicua
Es la que mejor se adapta a grandes áreas como Europa o los Estados Unidos. La retícula resultante es de arcos concéntricos
Azimutales o planares
Normal
Transversal
Oblicua
El punto de contacto puede ser los polos, un punto en el ecuador u otro punto entre ellos. También se denominan polar, ecuatorial u oblicua

Cilíndricas
Normal
Transversal
Oblicua
La primera usa las líneas de latitud como líneas de contacto; la segunda, los meridianos y la oblicua otras grandes líneas circulares
Cónicas
Normal
Transversal
Oblicua
Es la que mejor se adapta a grandes áreas como Europa o los Estados Unidos. La retícula resultante es de arcos concéntricos
Azimutales o planares
Normal
Transversal
Oblicua
El punto de contacto puede ser los polos, un punto en el ecuador u otro punto entre ellos. También se denominan polar, ecuatorial u oblicua

Normal
Transversal
Oblicua
Cilíndricas
La primera usa las líneas de latitud como líneas de contacto;
la segunda, los meridianos y la oblicua otras grandes líneas circulares
Cónicas
Es la que mejor se adapta a grandes áreas como Europa o
los Estados Unidos. La retícula resultante es de arcos concéntricos
Azimutales
o planares
El punto de contacto puede ser los polos, un punto en el ecuador
u otro punto entre ellos. También se denominan polar, ecuatorial u oblicua

Azimutales o planares
Cilíndricas
Cónicas
Normal
Transversal
Oblicua
Normal
Transversal
Oblicua
Normal
Transversal
Oblicua
Es la que mejor se adapta a grandes áreas como Europa o los Estados Unidos. La retícula resultante es de arcos concéntricos
El punto de contacto puede ser los polos, un punto en el ecuador
u otro punto entre ellos. También se denominan polar, ecuatorial u oblicua
La primera usa las líneas de latitud como líneas de contacto;
la segunda, los meridianos y la oblicua otras grandes líneas circulares
La proyección más utilizada a nivel global en la cartografía moderna es la de Mercator que es cilíndrica, transversal y tiene más de 450 años de vida. Pese a su longeva existencia, su implantación es tal que es la utilizada en las aplicaciones web de cartografía actuales como Google Maps, OpenStreetMap o BingMaps.
En ella, se divide la Tierra en meridianos y paralelos, con sesenta husos o zonas y es especialmente útil para la navegación porque preserva los ángulos y las direcciones de las rutas. No importa la zona del planeta que se represente, el norte y el sur aparecen siempre verticalmente; y el este y el oeste, horizontalmente, tal y como estamos acostumbrados a percibir.
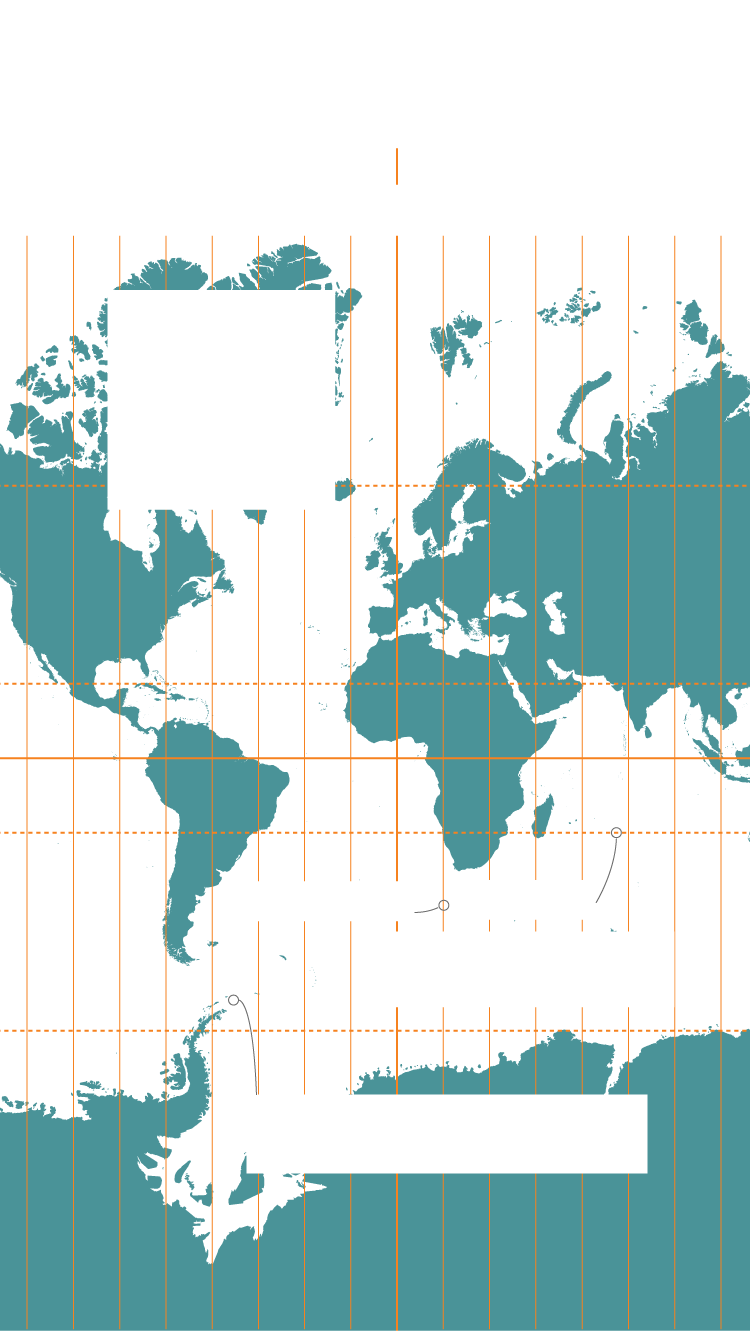
La Tierra se divide en 24 husos horarios, cada uno de 15 grados de longitud este u oeste. Tienen una hora de diferencia
HEMISFERIO OCCIDENTAL
HEMISFERIO ORIENTAL
135º
120º
105º
90º
75º
60º
45º
30º
15º
0º
15º
30º
45º
60º
75º
90º
105º
Meridiano de Greenwich
La proyección Mercator mantiene los ángulos precisos en cualquier punto del mapa
Trópico de Cáncer
Ecuador
Trópico de Capricornio
Paralelos
Meridianos
Son líneas rectas que se
cruzan en ángulos rectos
Las formas de pequeños objetos
se representan con precisión
HEMISFERIO OCCIDENTAL
HEMISFERIO ORIENTAL
180º
165º
150º
135º
120º
105º
90º
75º
60º
45º
30º
15º
0º
15º
30º
45º
60º
75º
90º
105º
120º
135º
150º
165º
180º
Meridiano de Greenwich
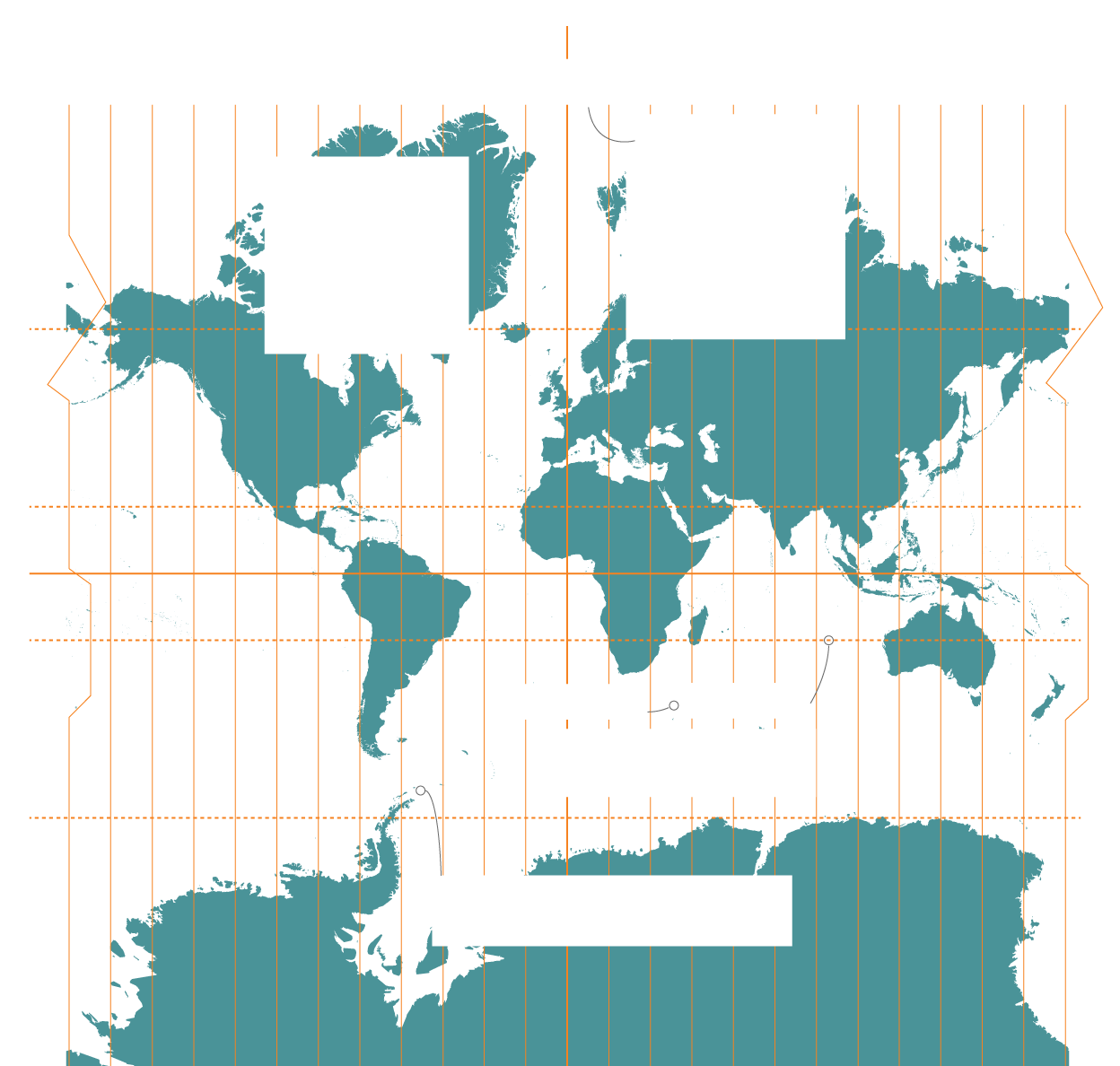
La Tierra se divide en 24 husos horarios, cada uno de 15 grados de longitud este u oeste. Tienen una hora de diferencia
La proyección Mercator mantiene los ángulos precisos en cualquier punto del mapa
Trópico de Cáncer
Ecuador
Trópico de Capricornio
Paralelos
Meridianos
Son líneas rectas que se
cruzan en ángulos rectos
Las formas de pequeños objetos
se representan con precisión

HEMISFERIO OCCIDENTAL
HEMISFERIO ORIENTAL
180º
165º
150º
135º
120º
105º
90º
75º
60º
45º
30º
15º
0º
15º
30º
45º
60º
75º
90º
105º
120º
135º
150º
165º
180º
Meridiano de Greenwich
La Tierra se divide en 24 husos horarios, cada uno de 15 grados de longitud este u oeste. Tienen una hora de diferencia
La proyección Mercator mantiene los ángulos precisos en cualquier punto del mapa
Sirve como punto de referencia para el coordinar el tiempo
Trópico de Cáncer
Ecuador
Trópico de Capricornio
Paralelos
Meridianos
Los horarios pueden ajustarse con fronteras por lo que no siempre siguen exactamente los meridianos
Son líneas rectas que se
cruzan en ángulos rectos
Las formas de pequeños objetos
se representan con precisión
HEMISFERIO OCCIDENTAL
HEMISFERIO ORIENTAL
180º
165º
150º
135º
120º
105º
90º
75º
60º
45º
30º
15º
0º
15º
30º
45º
60º
75º
90º
105º
120º
135º
150º
165º
180º
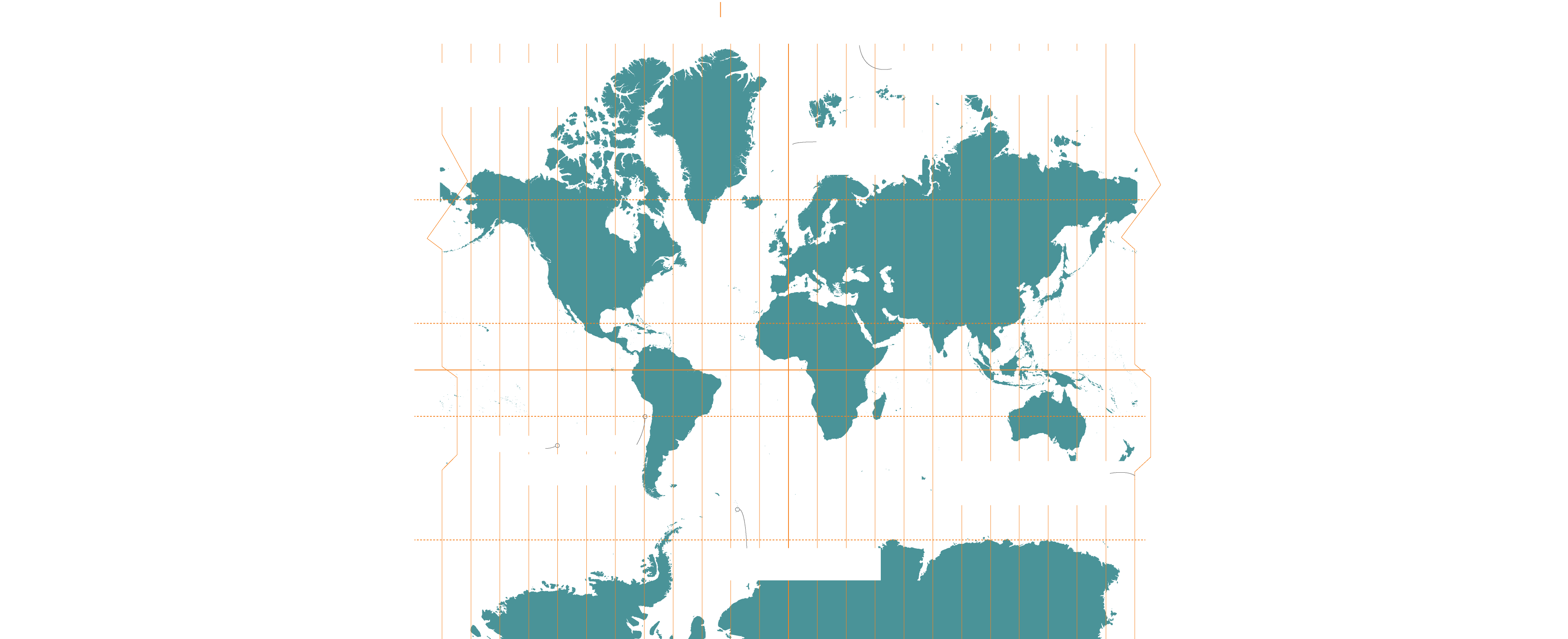
La Tierra se divide en 24 husos horarios, cada uno de 15 grados de longitud este u oeste. Tienen una hora de diferencia
La proyección Mercator mantiene los ángulos precisos en cualquier punto del mapa
Meridiano de Greenwich
Sirve como punto de referencia para el coordinar el tiempo
Trópico de Cáncer
Ecuador
Trópico de Capricornio
Paralelos
Meridianos
Son líneas rectas que se
cruzan en ángulos rectos
Los horarios pueden ajustarse con fronteras por lo que no siempre siguen exactamente los meridianos
Las formas de pequeños objetos
se representan con precisión
La proyección más utilizada es por tanto la Mercator que es la que, como hemos dicho, menos deforma la zona central del planeta pero claro, esto genera muchas imprecisiones. La más flagrante, la de los polos. Las regiones de alta latitud parecen mucho más grandes de lo que en realidad son. Así, la Antártida es reflejada como un continente que va de Alaska a Siberia. Ciertamente es un gran espacio terrestre pero también es el tercer continente más pequeño del planeta. Lo mismo sucede con Groenlandia, que aparece aproximadamente del tamaño de África cuando el continente africano es catorce veces la superficie de la isla ártica.

Proyección en
el Ecuador
Posición real con
deformación característica
1
1
Antártida
2
2
Groenlandia
2
2
1
1

Proyección en
el Ecuador
Posición real con
deformación característica
1
1
Antártida
2
2
Groenlandia
2
1
2
1

Proyección en el Ecuador
Posición real con deformación característica
1
1
Antártida
2
2
Groenlandia
2
1
2
1

Proyección en el Ecuador
Posición real con deformación característica
1
1
Antártida
2
2
Groenlandia
2
1
2
1
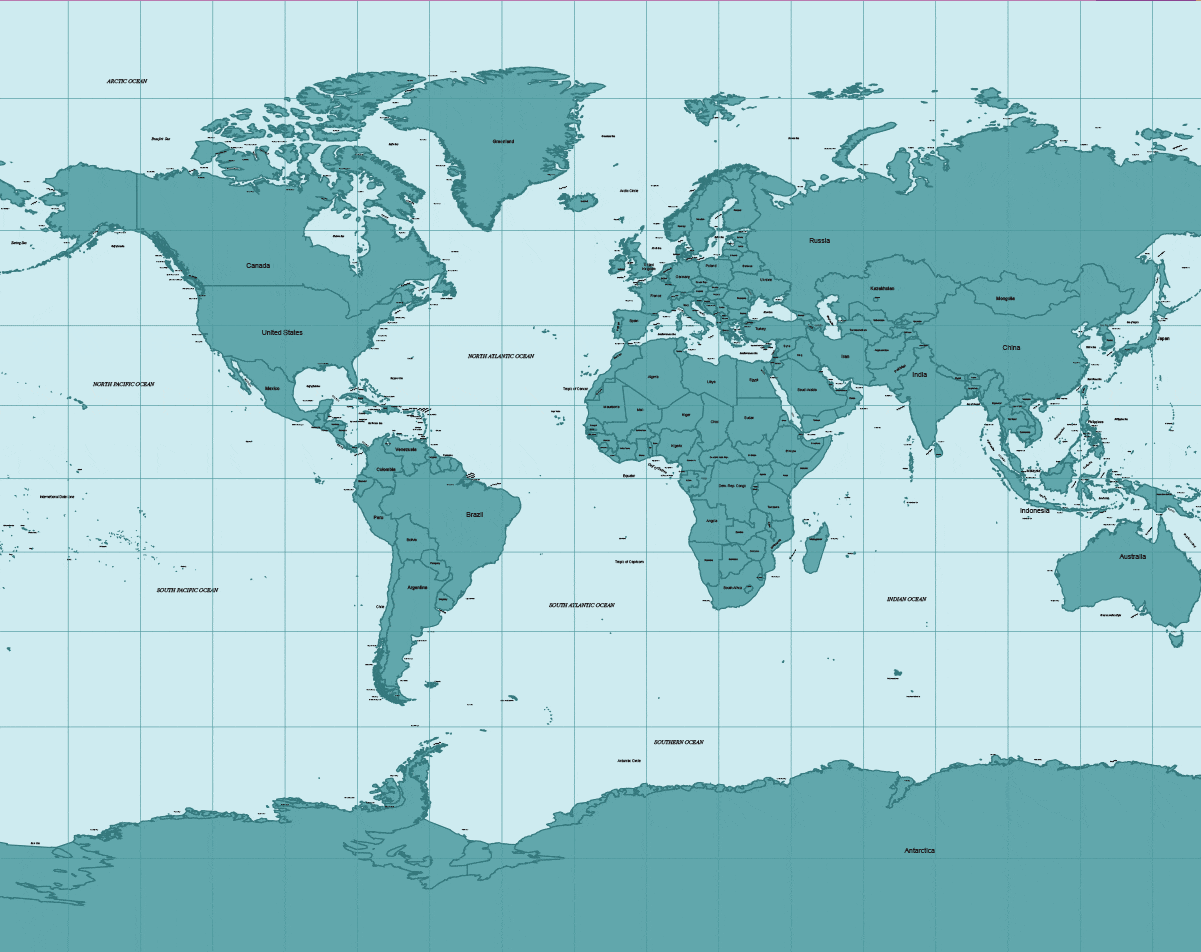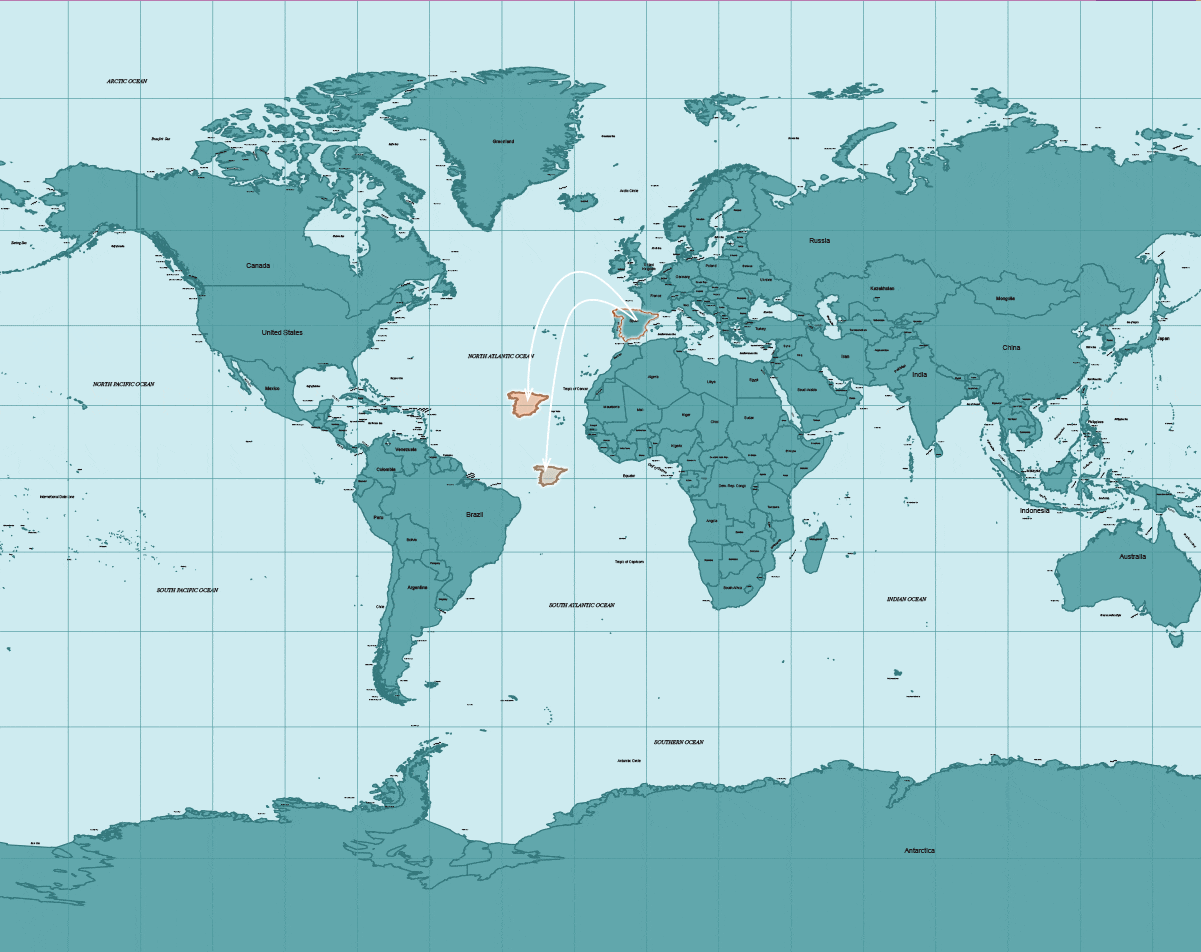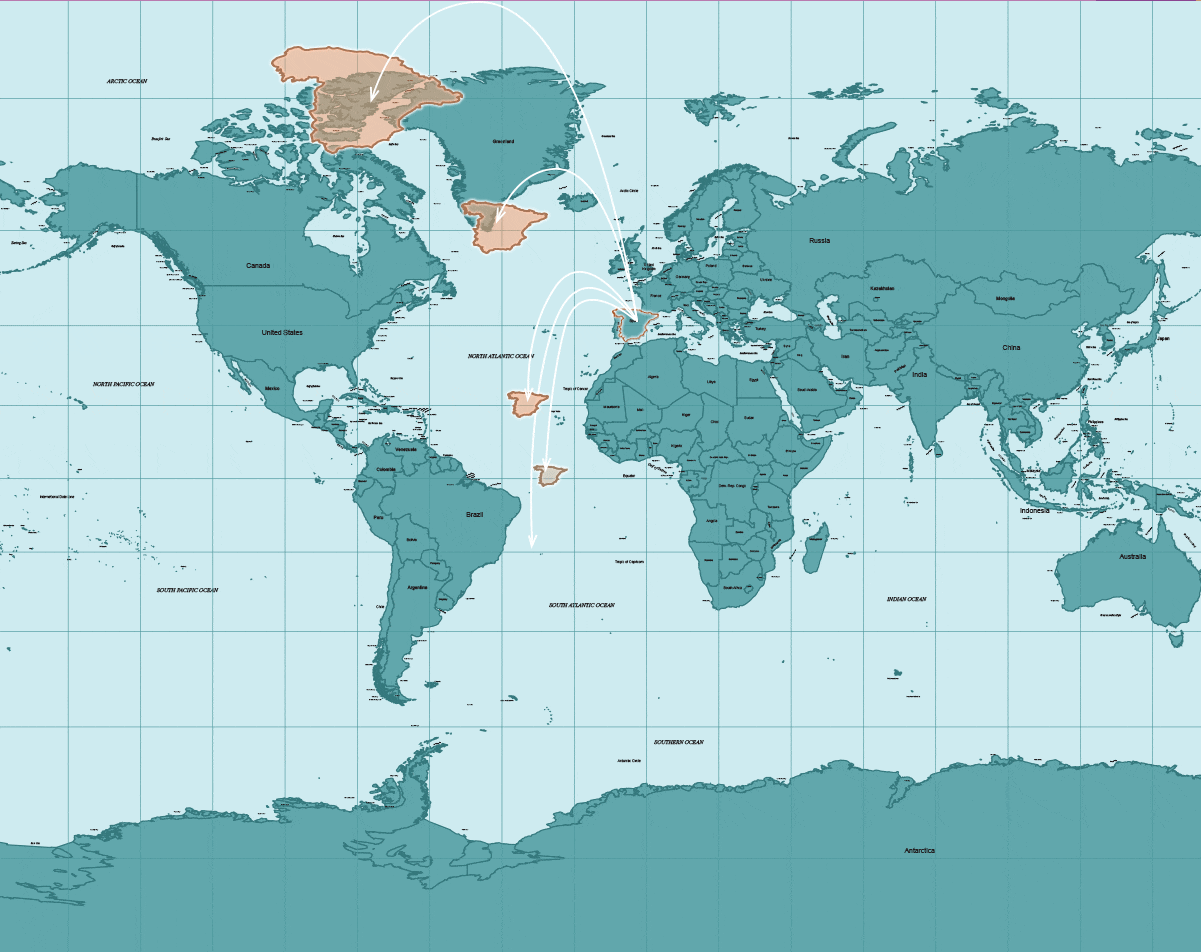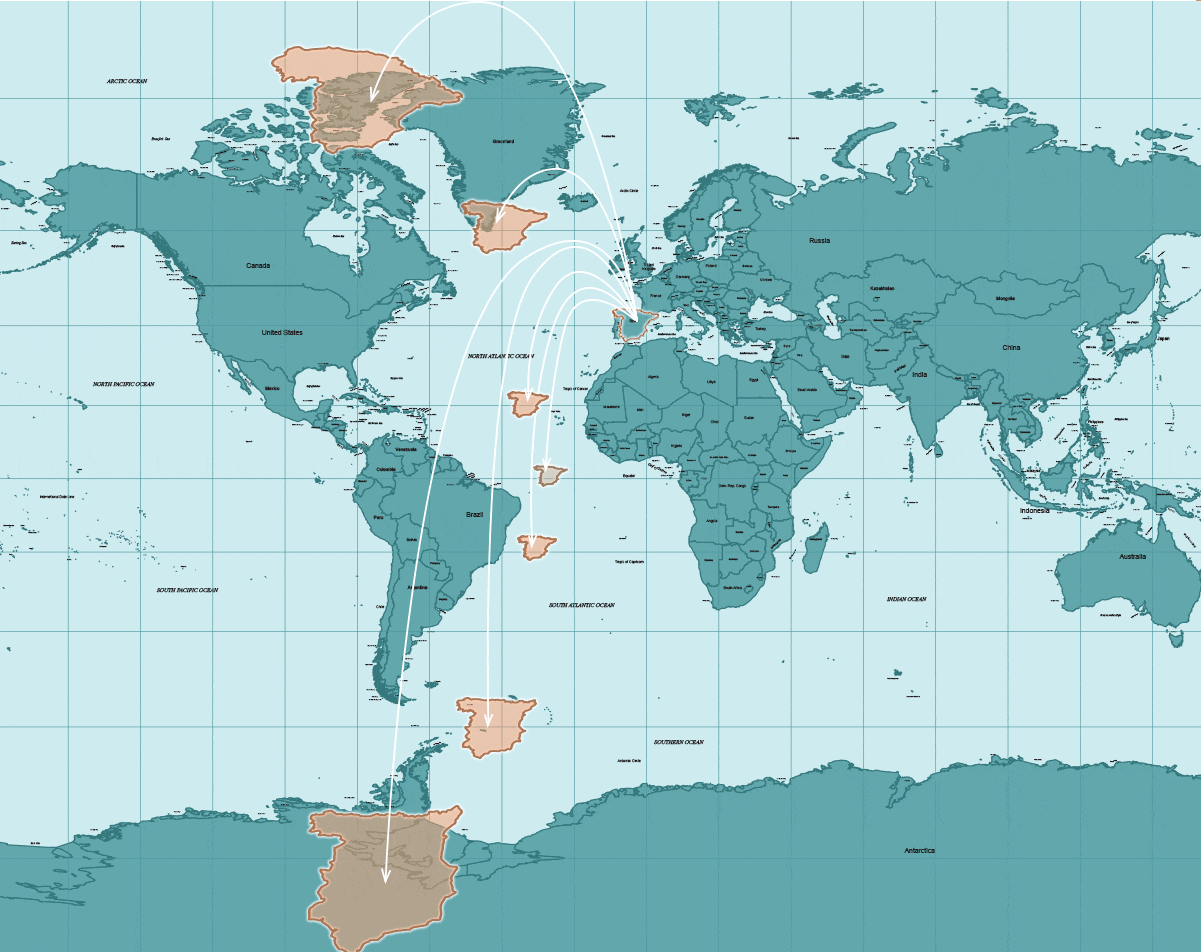
Un observador neófito podría concluir que los países europeos, por ejemplo, están representados con exactitud pero recordemos que sólo el área que está más próxima al Ecuador no sufre distorsiones significativas con la proyección Mercator; los más alejados son otra historia.
Por ejemplo, esta sería la representación (forma y tamaño) de España en este sistema si lo desplazamos por distintas zonas del mapa.

Cómo se vería España (peninsular)
si estuviera en:
1
En el Ecuador
Trópico de Cáncer
2
3
Círculo Polar Ártico
Casquete ártico
4
5
Trópico de Capricornio
6
Círculo Polar Antártico
7
Antártida
4
3
2
1
5
6
7
4
1
2
3
7
6
5

Cómo se vería España (peninsular)
si estuviera en:
1
En el Ecuador
5
Trópico de
Capricornio
Trópico de Cáncer
2
6
Círculo Polar
Antártico
3
Círculo Polar Ártico
7
Casquete ártico
4
Antártida
4
3
2
1
5
6
7
4
1
2
3
7
6
5

Cómo se vería España (peninsular) si estuviera en:
Trópico de Cáncer
En el Ecuador
Círculo Polar Ártico
Casquete ártico
1
3
4
2
5
6
7
Antártida
Trópico de Capricornio
Círculo Polar Antártico
4
3
2
1
5
6
7
7
4
6
5
1
2
3

Cómo se vería España (peninsular) si estuviera en:
Trópico de Cáncer
En el Ecuador
Círculo Polar Ártico
Casquete ártico
1
3
4
2
5
6
7
Antártida
Trópico de Capricornio
Círculo Polar Antártico
4
3
2
1
5
6
7
7
4
6
5
1
2
3
Curioso, ¿verdad? Las distorsiones son mucho más pronunciadas en otros países. Por ejemplo, Rusia parece más grande que todo el continente y africano mientras que América del Norte, con la proyección Mercator, es mucho más alta de norte a sur y con sus regiones árticas muy estiradas. También es chocante el caso de Madagascar y Gran Bretaña que parecen del mismo tamaño pero la isla africana es realmente más del doble de grande que el territorio británico. De hecho, toda África aparece empequeñecida si la comparamos por ejemplo con América del Sur. Su superficie asemeja ser similar pero el continente vecino es un 150% más grande. Además, Canadá y Estados Unidos empequeñecen considerablemente si tenemos en cuenta su dimensión real.

Posición real con
deformación característica
Proyección
en el Ecuador
1
1
Canadá
2
2
Estados Unidos
Argentina
3
3
4
4
Islandia
5
5
Reino Unido
6
6
Finlandia
Madagascar
7
7
8
8
China
9
9
Rusia
6
4
9
1
5
2
8
3
1
2
9
8
6
5
4
7
7
3

Posición real con
deformación característica
Proyección
en el Ecuador
1
1
Canadá
2
2
Estados Unidos
Argentina
3
3
4
4
Islandia
5
5
Reino Unido
6
6
Finlandia
Madagascar
7
7
8
8
China
9
9
Rusia
6
4
9
1
5
2
8
3
1
2
9
8
6
5
4
7
7
3

Posición real con
deformación característica
Proyección
en el Ecuador
Posición real con
deformación característica
Proyección
en el Ecuador
5
5
Reino Unido
1
1
Canadá
6
6
2
2
Finlandia
Estados Unidos
Argentina
Madagascar
7
7
3
3
8
8
4
4
Islandia
China
9
9
Rusia
6
4
9
1
5
2
8
3
1
2
9
8
6
5
4
7
7
3

Posición real con
deformación característica
Proyección
en el Ecuador
Posición real con
deformación característica
Proyección
en el Ecuador
5
5
Reino Unido
1
1
Canadá
6
6
2
2
Finlandia
Estados Unidos
Argentina
Madagascar
7
7
3
3
8
8
4
4
Islandia
China
9
9
Rusia
6
4
9
1
5
2
8
3
1
2
9
8
6
5
4
7
7
3
Está claro que la cartografía es inexacta. Se elija el sistema de proyección que se elija, no existe manera de trasladar un mapa esférico a un plano sin que se generen distorsiones. Incluso cuando se realizan mapas a partir de ortofotos (fotografías aéreas) hay que hacer correcciones en las imágenes por la distorsión de la lente de la cámara, la altura, etc. Gran cantidad imprecisiones se concentran pues en las representaciones planimétricas de la Tierra; sin embargo, tendemos a asumir que son fiel reflejo del conocimiento y que con el avance de la cartografía moderna no existen fallos o estos son mínimos. Es cierto, que ha habido muchísimos avances incluso desde la aparición del primer atlas moderno, el famosísimo Theatrum Orbis Terrarum, de Abraham Ortelius.
Pero hay más. Mucho más. Los mapas se han utilizado desde el origen de los tiempos para impulsar o representar influencias e intereses. Los poderes políticos reflejan en ellos intenciones que parecen verdades incontrovertibles. Un cartógrafo puede cambiar elementos como los límites territoriales tan fácilmente como puede cambiar las proyecciones en un mapa.
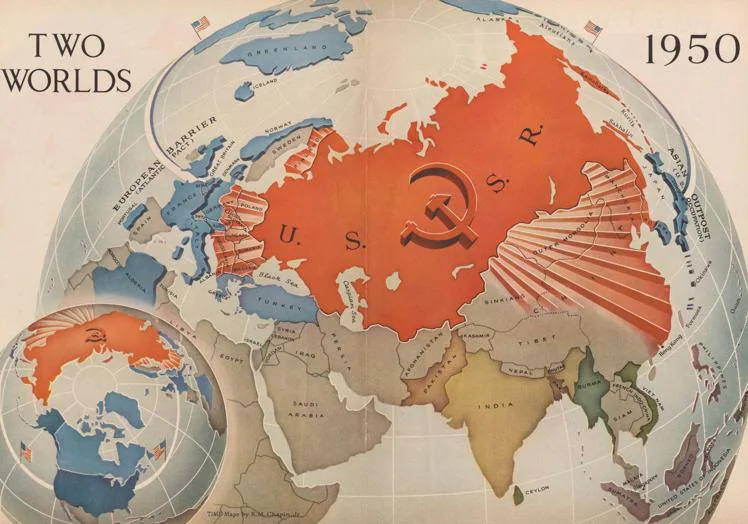
Así, durante la Guerra Fría se utilizaron un sinfín de mapas como arma de propaganda política. El conocido como 'Dos Mundos', publicado en la revista Time, utilizaba una azimutal desde el polo norte para enfatizar la peligrosa cercanía de la Unión Soviética con los Estados Unidos. En el mapa las extensiones de la URSS quedan maximizadas con una perspectiva cartográfica alarmista que ayudó a 'convencer' a los estadounidenses para que apoyaran los costosos programas anticomunistas del momento (Plan Marshall y doctrina Truman) frente al 'gran enemigo rojo'.
Los ejemplos del uso político de la cartografía continúan en la actualidad. Como el que se puedo ver hace unos meses cuando China presentó su nuevo mapa, con una proyección vertical, que incluía su controvertida 'línea de 10 puntos'. Esencialmente incluía la totalidad del mar de China y de Taiwán como propios.
Si hablamos de fronteras nacionales, asumir una línea u otra, en las zonas conflictivas o en las que hay intereses en liza puede ser un tema políticamente espinoso pero además es una situación que algunas empresas deciden esquivan hábilmente.
Así, la todopoderosa Google, con su servicio en línea de GoogleMaps, generaba hasta hace bien poco distintos atlas geográficos según el lugar desde donde se accedía. Las fronteras nacionales se trasladaban de un sitio a otro para demostrar que la empresa apoyaba la postura del gobierno local, sea cual fuera. Eran versiones que se movían unos kilómetros para evitar el posicionamiento político de la firma. Ante las críticas que provocó esta actuación la magnate estadounidense empezó a cambiar gradualmente sus mapas tras la pandemia.
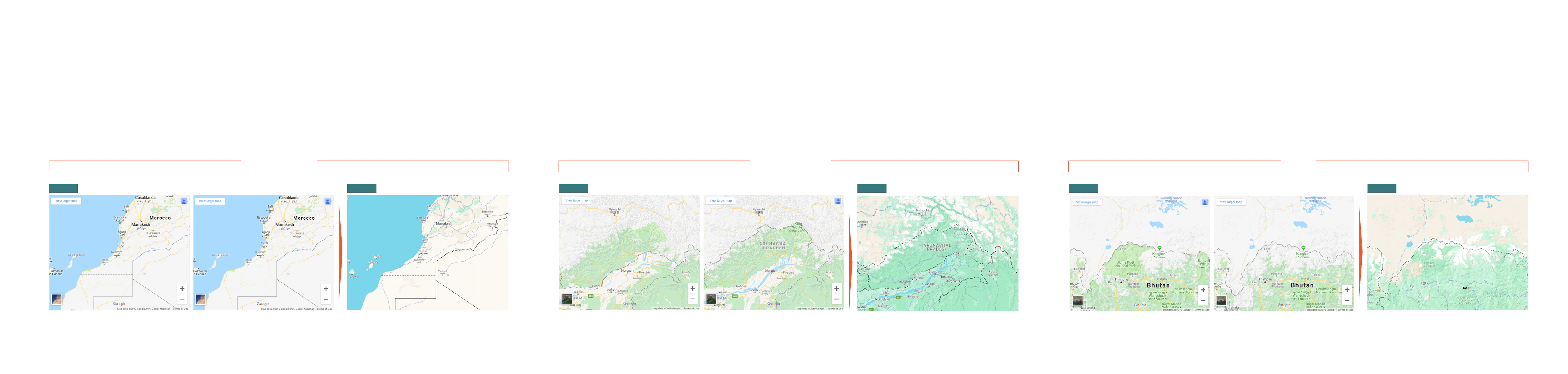
SÁHARA OCCIDENTAL
ARUNACHAL PRADESH
BUTAN
Para Google Maps no existía si entrabas desde Marruecos
Una de las regiones en disputa entre la República Popular China e India
La frontera entre China y Bután presentaban aspectos diferentes
2019
Hoy
2019
Hoy
2019
Hoy
Desde España
Desde China
Desde Bután
Desde Marruecos
Desde India
Desde China
Obviamente, la conducta de Google era una maniobra comercial para no perder el mercado local de los servicios que ofrece a los obiernos que se diputan tierras pero esto planteó y sigue planteando dos cuestiones muy espinosas. Por un lado, el poco decoro a la hora de tener dos posturas contrapuestas por intereses comerciales y otro más esquivo, la influencia que se ejerce en el imaginario colectivo al mostrar una realidad que no es tal sin que el usuario sea consciente de ello. La mayoría de personas somos consumidores involuntarios de mapas y asumimos que los cartógrafos que los han diseñado son competentes y veraces.
Los mapas nunca han sido, ni siguen siendo hoy en día, sólo proyecciones del conocimiento espacial, sino que también son imágenes del mundo y sobre todo son un conjunto de intenciones que evidenciamos con la cartografía con el disfraz de verdad absoluta. En la actualidad, los mapas forman parte de nuestra vida, los llevamos en nuestros bolsillos y podemos consultar cualquier lugar del mundo con un solo clic. Por eso hay que ser especialmente cauto y escéptico con ellos. Aunque parezcan científicos, exactos y veraces no pueden mostrar la realidad tal cual es y además pueden esconder algunas mentiras insidiosas.
Publicidad
Cristina Cándido, José A. González y Sara I. Belled
Cristina Cándido y Álex Sánchez
Borja Crespo y Lidia Carvajal
Esta funcionalidad es exclusiva para suscriptores.
Reporta un error en esta noticia
Los mapas nos mienten
Comentar es una ventaja exclusiva para suscriptores
¿Ya eres suscriptor?
Inicia sesiónNecesitas ser suscriptor para poder votar.